El Fin de las Matemáticas: Un Descubrimiento sobre los Infinitos Revoluciona la Ciencia

Inicio / El Fin de las Matemáticas: Un Descubrimiento sobre los Infinitos Revoluciona la Ciencia

Un hallazgo matemático desafía conceptos fundamentales y abre nuevas puertas al estudio del infinito

Redacción/CAMBIO22

El concepto de “infinito” puede parecer sencillo a simple vista, pero se torna considerablemente más complejo a medida que profundizamos en su naturaleza. Esta situación se debe a que, aunque el infinito se concibe como una secuencia interminable de números, en realidad está compuesto por una jerarquía de infinitos, cada uno de los cuales presenta un grado de complejidad superior.

De hecho, recientemente, científicos de la Universidad Tecnológica de Viena y de la Universidad de Barcelona identificaron dos nuevos tipos de infinito, conocidos como “cardinales exactos” y “ultra exactos”. Este descubrimiento desafía la estructura jerárquica tradicional de los infinitos, exhibiendo propiedades que no se alinean con la comprensión convencional.

Los detalles de estos conjuntos infinitos fueron presentados en un artículo publicado en el servidor de preimpresión arXiv, aún no revisado por pares.

Descubren dos nuevos tipos de infinito: cardinales exactos y ultra exactos

Recientemente, matemáticos de la Universidad Tecnológica de Viena y de la Universidad de Barcelona identificaron dos nuevos tipos de infinito, conocidos como cardinales exactos y ultra exactos. Estos conjuntos infinitos tienen propiedades inusuales que los apartan de la jerarquía estándar de infinitos establecida en la teoría matemática tradicional.

Tradicionalmente, los matemáticos clasifican los infinitos dentro de una estructura jerárquica basada en su tamaño, pero los nuevos descubrimientos no siguen esta estructura de manera sencilla.

Según Juan Aguilera, coautor del estudio de la Universidad Tecnológica de Viena, estos infinitos son tan complejos que no se pueden ordenar dentro de la jerarquía convencional de cardinales. En lugar de simplemente ser más grandes que los cardinales tradicionales, los cardinales exactos y ultra exactos interactúan con otros conceptos de infinito de formas extrañas e inesperadas.

Este descubrimiento sugiere que el concepto de infinito podría ser aún más complejo de lo que se pensaba, y abre nuevas posibilidades para la comprensión de los conjuntos infinitos en matemáticas.

Desafíos en el axioma de la elección y la teoría de conjuntos

El concepto de infinito en matemáticas está íntimamente relacionado con un principio fundamental conocido como el axioma de la elección, crucial en la teoría de conjuntos. Este axioma sostiene que es posible crear nuevos conjuntos seleccionando elementos de otros conjuntos, lo que genera una jerarquía bien establecida de los infinitos.

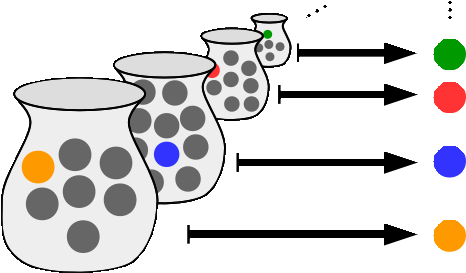De forma convencional, los infinitos se agrupan en tres categorías principales: los que se ajustan a los axiomas de la teoría de conjuntos, aquellos tan grandes que parecen pertenecer a una especie de “matemáticas del caos”, y los que se encuentran en una región intermedia entre estos dos extremos.